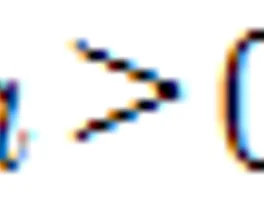 지수함수 정의, 기초공식 - 안성환쌤의 연역적수학
1. 지수함수의 정의 이고 일 때, 함수 을 를 밑으로 하는 의 지수함수라 한다. 2. 지수함수 의 성질(1) 정의구역은 실수 전체의 집합 (2) 치역은 양의 실수 전체의 집합(3) 일 때, 의 값이 증가하면 의 값도 증가한다. 즉, 이면 이다. 이면 의 값이 증가하면, 의 값은 감소한다. 즉, 이면 이다.(4) 그래프는 점 , 를 지난다.(5) 점근선은 축()(6) 의 그래프와 의 그래프는 축에 대하여 대칭이다. 지수함수 (, )의 그래프를① 축에 대하여 대칭이동 ⇨ ② 축에 대하여 대칭이동 ⇨ ③ 원점에 대하여 대칭이동 ⇨ (7) 지수함수 (, )의 그래프를 축의 방향으로 만큼, 축의방향으로 만큼 평행이동하면 이다.
지수함수 정의, 기초공식 - 안성환쌤의 연역적수학
1. 지수함수의 정의 이고 일 때, 함수 을 를 밑으로 하는 의 지수함수라 한다. 2. 지수함수 의 성질(1) 정의구역은 실수 전체의 집합 (2) 치역은 양의 실수 전체의 집합(3) 일 때, 의 값이 증가하면 의 값도 증가한다. 즉, 이면 이다. 이면 의 값이 증가하면, 의 값은 감소한다. 즉, 이면 이다.(4) 그래프는 점 , 를 지난다.(5) 점근선은 축()(6) 의 그래프와 의 그래프는 축에 대하여 대칭이다. 지수함수 (, )의 그래프를① 축에 대하여 대칭이동 ⇨ ② 축에 대하여 대칭이동 ⇨ ③ 원점에 대하여 대칭이동 ⇨ (7) 지수함수 (, )의 그래프를 축의 방향으로 만큼, 축의방향으로 만큼 평행이동하면 이다.