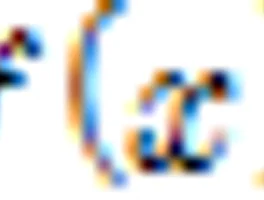로피탈의 정리 증명 - 안성환쌤의 연역적수학
로피탈의 정리 증명하는 법. 1) 중간값의 정리함수 가 폐구간 [a, b]에서 연속이고 일 때, 와 사이의 임의의 값 에 대하여 를 만족하는 가 개구간 (a, b)안에 적어도 하나 존재한다. 2) 롤의 정리 함수 가 폐구간 [a, b]에서 연속이고, 개구간 (a, b)에서 미분가능하며, 이면 인 가 개구간 안에 적어도 하나 존재한다. 3) 평균값의 정리 함수 가 폐구간 [a, b]에서 연속이고, 개구간 (a, b)에서 미분가능하면인 가 개구간 안에 적어도 하나 존재한다. 4) Cauchy(코시)의 평균값의 정리 함수 와 가 폐구간 [a, b]에서 연속이고, 개구간 (a, b)에서 미분가능하고, 구간 내의 모든 점에서 이고, 이면,인 가 개구간 (a, b)안에 적어도 하나 존재한다. 5) 부정형 에 대한 ..
고3 6월 모평 수학범위 - 안성환쌤의 연역적수학
6월 모의고사 수학범위 A형 수학I 전범위미통기 : 함수의 극한, 연속, 미분계수, 다항함수의 미분법 B형수학I 전범위수학II 전범위적분과 통계 : 적분법, 순열과 조합기하와 벡터 : 일차변환, 이차곡선 이제 슬슬....여집합을 보는 것이 빠르다... A형적분법. 순열과 조합, 확률, 통계 B형기하와 벡터:공간도형, 벡터,적분과 통계: 확률, 통계
