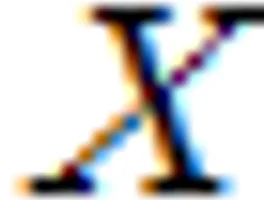 연속확률변수 기초공식, 평균, 분산 표준편차 공식 - 안성환쌤의 연역적 수학
1 연속확률변수의 평균, 분산, 표준편차연속확률변수 가 취할 수 있는 값의 범위가 이고 확률밀도함수 일 때, 의 평균 , 분산 , 표준편차 는 다음과 같다. (1) 평균 : (2) 분산 : 또는 (3) 표준편차 : 무언가 특이한 공식같이 생겼다. 평균을 구하는데 를 적분하다니!!! 그런데 따지고 보면 이산확률분포의 평균, 분산과 똑같은 것이다. 이산확률분포표에서 평균은 어찌 구했는가? 확률변수 확률 들의 총 합이다. 연속확률변수에서 확률변수는 이고, 확률은 연속적인 값들이므로 총합은 적분을 통해 구할 수 있다!! 요렇게 이해해주면 되겠다~ 2 연속확률변수 의 평균, 분산, 표준편차연속확률변수 (는 임의의 상수)의 평균 , 분산 , 표준편차 는 다음과 같다. (1) (2) (3)
연속확률변수 기초공식, 평균, 분산 표준편차 공식 - 안성환쌤의 연역적 수학
1 연속확률변수의 평균, 분산, 표준편차연속확률변수 가 취할 수 있는 값의 범위가 이고 확률밀도함수 일 때, 의 평균 , 분산 , 표준편차 는 다음과 같다. (1) 평균 : (2) 분산 : 또는 (3) 표준편차 : 무언가 특이한 공식같이 생겼다. 평균을 구하는데 를 적분하다니!!! 그런데 따지고 보면 이산확률분포의 평균, 분산과 똑같은 것이다. 이산확률분포표에서 평균은 어찌 구했는가? 확률변수 확률 들의 총 합이다. 연속확률변수에서 확률변수는 이고, 확률은 연속적인 값들이므로 총합은 적분을 통해 구할 수 있다!! 요렇게 이해해주면 되겠다~ 2 연속확률변수 의 평균, 분산, 표준편차연속확률변수 (는 임의의 상수)의 평균 , 분산 , 표준편차 는 다음과 같다. (1) (2) (3)