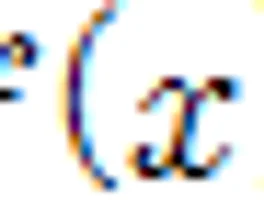 f(x)란 무엇인가 -안성환쌤의 연역적수학
란 무엇인가? 대부분의 학생들의 대답 : ...함수요! 특이한 학생들의 대답 : 설리가 진리요.. 는 함수가 아니다. 그냥, 가 들어간 식! (여기에서 는 무엇인가?---------변수이다. 내가 마음대로 숫자를 대입할 수 있다. 이라면, , ....요런거다.) 그게 끝이다. 요렇게.. , , , , .... 그냥 가 들어간 식이다! (뭐...이렇게, 가 들어가지 않을 수도 있긴 하다..) 이라고 쓰면 방정식이 된다. 라고 쓰면 함수......가 아니다. 그냥 와 의 관계식이다. 함수 라고 써야 함수이다..... 와 의 관계식은 함수라고 봐도 고등학교 수학에서야 무방하겠지... 꼭 를 써야할 필요도 없다. , , , ... 그냥 식에 이름을 붙여준 것 뿐이다.
f(x)란 무엇인가 -안성환쌤의 연역적수학
란 무엇인가? 대부분의 학생들의 대답 : ...함수요! 특이한 학생들의 대답 : 설리가 진리요.. 는 함수가 아니다. 그냥, 가 들어간 식! (여기에서 는 무엇인가?---------변수이다. 내가 마음대로 숫자를 대입할 수 있다. 이라면, , ....요런거다.) 그게 끝이다. 요렇게.. , , , , .... 그냥 가 들어간 식이다! (뭐...이렇게, 가 들어가지 않을 수도 있긴 하다..) 이라고 쓰면 방정식이 된다. 라고 쓰면 함수......가 아니다. 그냥 와 의 관계식이다. 함수 라고 써야 함수이다..... 와 의 관계식은 함수라고 봐도 고등학교 수학에서야 무방하겠지... 꼭 를 써야할 필요도 없다. , , , ... 그냥 식에 이름을 붙여준 것 뿐이다.