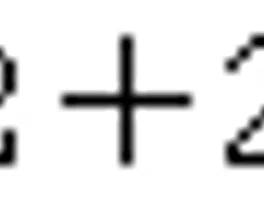지수법칙1, 0의 0승, 1의 0승, 2의 0승... - 안성환쌤의 연역적수학
0의 0승, 2의 0승.... a의 0승 – 지수법칙1 수학자는 게으른 동물이다. 어찌나 게으른지! 도 쓰기 귀찮아서! 곱셈기호를 만들었다. 근데, 만들고 보니 누군가 물었다. 는 쓰기 귀찮지 않냐고! 그래서 만들었다!두둥 이것이 지수!(많은 변천사가 있었지만, 최종적인 표기법은 가우스!가 만드심) 자, 지수를 읽어보자. 2를 4번 곱한다. 이름표를 붙여야 의사소통하기 좋겠지?에서 2를 ‘밑’이라 하고 4를 ‘지수’라고 한다! 처음의 지수는 자연수에서만 정의됐었다. 왜냐하면 밑을 곱하는 ‘갯수’였기 때문이다! 수학자는 그냥 두지 않는다.자연수에 한정하지 않고 정수, 유리수까지 확장해 버린다...... 자, 을 풀어보자. 알아야 할 것은 단지 이것 뿐!지수를 말로 풀어보자고!2를 2번 곱한 숫자에, 다시 ..
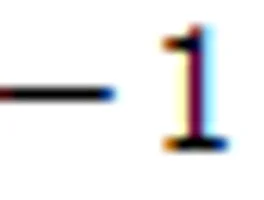복소수 허수 공식 - 안성환쌤의 연역적수학
복소수공식, 복소수의 기초 허수단위제곱하여 이 되는 수를 로 나타내고, 이를 허수단위라 한다. 즉, 복소수의 사칙연산가 실수일 때, (1) (2) (3) (4) (단, ) 분자, 분모에 분모 의 결레복소수 를 각각 곱하여 정리한다. 실수부와 허수부는 물과 기름이다! 따로 따로 계산하는 것만 기억하자 켤레복소수(1) 복소수 (는 실수)에 대하여 를 의 켤레복소수라 하고, 로 나타낸다. 즉, (2) 켤레복소수의 성질 두 복소수 에 대하여 ①② (복부호동순)③④(단, )⑤는 실수⑥는 실수 ③~⑥이 까먹기 좋다. 고2, 고3때까지 기억하도록 노력하자 음수의 제곱근(1) 일 때, 이고, 음수 의 제곱근은 이다.(2) 이면 이면 또는 또는 (3) 이면 이면 또는 고1때는 당연하거니와, 이후에도 종종 출제된다.암기하..
