평면에서 곡선의 길이
(1) 곡선 ,
의 길이
(2) 곡선
의 길이
(2)번 공식은 사실, (1)번 공식과 같다.
(1)번 공식에 ,
를 적용해보면
↓ ↓
곡선의 길이의 증명

,
의 길이
곡선 ,
의 길이
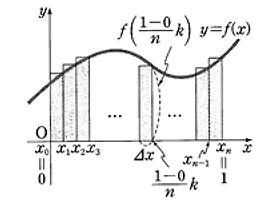
은 오른쪽 [그림 1]과 같이 시각
에 대하여
좌표가
이고,
좌표가
인 점
가 좌표평면 위에서 시각
부터
까지 움직인 거리와 같다.
이때 오른쪽 [그림 2]와 같이 매개변수가 부터
까지 변할 때, 점
는 점
로 움직인다고 하면,
의 증분
가 충분히 작을 때
의 증분
은 선분
의 길이와 거의 같다.
따라서 곡선 ,
의 길이
은
㉠

의 길이
함수
는 매개변수
를 이용하여 다음과 같이 나타낼 수 있다.
,
㉠에 의하여 곡선
,
의 길이
은
'적분' 카테고리의 다른 글
| 무한급수와 정적분 - 안성환쌤의 연역적수학 (0) | 2015.06.08 |
|---|---|
| 입체적분 이해- 안성환쌤의 연역적수학해 (0) | 2015.05.29 |
| 치환적분, 치환요령- (0) | 2015.05.29 |
| 삼차함수 넓이공식- 안성환쌤의 연역적수학식 (0) | 2015.05.29 |
| 이차함수 넓이공식- (0) | 2015.05.29 |