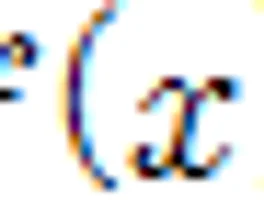행렬 곱셈
행렬곱셈의 정의
두 행렬  에 대하여 행렬
에 대하여 행렬  의 열의 개수와 행렬
의 열의 개수와 행렬  의 행의 개수가 같을 때,
의 행의 개수가 같을 때,  의 제
의 제  행의 성분과
행의 성분과  의 제
의 제  열의 성분을 차례로 곱하여 더한 값을 (
열의 성분을 차례로 곱하여 더한 값을 ( )성분으로 하는 행렬을 행렬
)성분으로 하는 행렬을 행렬  와
와  의 곱이라 하고, 기호로
의 곱이라 하고, 기호로  로 나타낸다.
로 나타낸다.
(행렬 | (행렬 | (행렬 | ||
( | ( | ( |
행렬만 기억하면 된다.
근데 행이 가로였나?세로였나??
열이 가로였나?세로였나??
요것만 기억하면 되겠다.
행:가로 행
렬:세로 열
첫 번째 행렬의 ‘행’과, 두 번째 행렬의 ‘열’을 각각 곱해서 더해준 것이
원소가 된다.
첫 번재 행렬의 2번째 행, 두 번째 행렬의 3번째 열을 연산하면
(2, 3)원소가 나온다.
각각 곱해서 더해주는 연산법에 의해
첫 번째 행렬의 ‘행’에 있는 숫자의 개수와 두 번째 행렬의 ‘열’에 있는 숫자의 개수가 같아야 연산이 가능하다.
두 행렬 에 대하여
의 곱
를 구해보면
아아아...이제 행렬도 올해로 마지막 강의겠구나....뭔가 아쉽다.....
'수학의 기본개념' 카테고리의 다른 글
| 행렬 곱셈, 거듭제곱 암산 공식 - 안성환쌤의 연역적수학 (3) | 2015.06.02 |
|---|---|
| f(x)란 무엇인가 -안성환쌤의 연역적수학 (0) | 2015.05.30 |
| 수직선, 1차원 - 안성환쌤의 연역적수학 (0) | 2015.05.29 |
| 가우스x [x] 풀이요령 - 안성환쌤의 연역적수학 (0) | 2015.05.29 |
| 삼각형 넓이공식 - 안성환쌤의 연역적수학 (0) | 2015.05.29 |