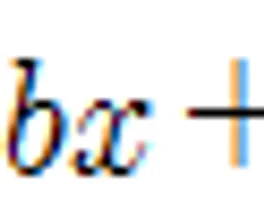이차방정식 근의 공식
는 몇인가?
너무 쉽네~
조금 더 어렵게,
미지수의 차수가 1인 방정식을 일차방정식이라 한다.
그렇다면 모든 일차방정식을 한번에 풀어주는 공식을 만들어 볼까?
이 모든 일차방정식이다.
우변에 숫자가 있으면 이항해서 합쳐주면 된다. 가 좌변, 우변에 있어도 이항해서 정리할 수 있다!
이 경우에 는 몇인가?
간단하다!
이것이 일차방정식의 근의 공식이다.
그렇다면~
이제 2차 방정식의 근의 공식을 만들어 보자.
일단 모든 이차방정식의 기준형태를 잡자.
모든 이차방정식은 위와 같이 정리할 수 있다.
여기에서 중요한 것은!
,
,
는 모두 상수이다.
이제부터~~풀어보자.
| ||
| ||
한편 가 짝수일 때는 조금 더 약분이 가능하다.
가 짝수이므로
라 하면
사실 분모분자를 2로 약분한 것일 뿐이다.
몰라도 문제푸는데 아무런 지장이 없다.
단지 ‘아주 조금’ 더 빨리 푸는 공식일 뿐.
'고등 1년수학' 카테고리의 다른 글
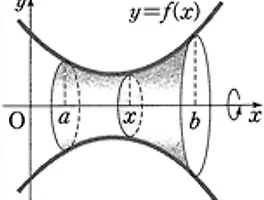
| 회전체 부피 적분공식- 안성환쌤의 연역적수학식 (0) | 2015.05.29 |
|---|---|
| 이차방정식의 근과 계수와의 관계 - 안성환쌤의 연역적수학 (0) | 2015.05.29 |
| 이차방정식 근의 공식 활용- 이차방정식 두 근의 거리 - 안성환쌤의 연역적수학 (0) | 2015.05.29 |
| 일대일함수 일대일대응 정의, 구별 - 설공아빠 (0) | 2015.05.29 |
| 함수의 갯수 - 안성환쌤의 연역적수학 (0) | 2015.05.29 |